لتمثيل العُقد على مستوى نستخدم "رسم تخطيطي للعُقد". ونبدأ من مسقط للعقدة على المستوى ونميز الممر العلوي من الممر السفلي، (الصورة أسفله) ويكون الأمر مفيدا إذا تم فحص العقد ذات المركبات المتعددة والمسماة ضفيرة. لأنها تمثل أيضا برسوم تخطيطة. ويعتبر مقال جاوس الثاني عن العُقد (والضفائر) ذو طبيعة تركيبية، ويصف طريقه لعمل شفرة للرسوم الخطيطية لكل منهم، وتعتبر ذريقة جاوس أساسية في هذا المجال.
وأول من نزع لعمل تصنيف منظم للعُقد هو بيتر جوفري تيه Peter Guthrie Tait (1831-1901)
متأثرا بنظرية اللورد كلفين Lord Kelvin، والتي من خلالها تعتبر الذرات عُقد في الأثير، لقد قرر تيه أن نظرية العُقد أساسية في دراسة الفيزياء وكرس لها الثلاثين عاماً الأخيرة من حياته. لقد عرف عدة مفاهيم مازالت مستخدمة إلى الآن. وقبل كل شيء أدخل "قياس الترتيب" للعُقدة.
والأهم في كل ذلك هو "عدد التقاطعات" لكل عُقدة يعرف على أنه أصغر عدداً من التقاطعات لرسم تخطيطي يمثل عُقدة، وإذا كانت N عقدة، سنسمي مجموع N عدد التقاطعات ونقول عُقد تافهة للدائرة غير المعقودة.
وعدد تقاطعات الدائرة التافهة هو الصفر العُقد غير التافهة الأكثر بساطة هي بالفرنسية الـ trèfle
لقد عرف تيه أيضا مفهوم الجمع للعقد، (انظر الصورة) ولكي تكون هذه العملية معرفة تعريفا جيدا يجب أن "نوجه" العُقد التي نجمعها، بمعنى آخر نزودهم باتجاه للمسار. فإذا كانت N عقدة فإن مجموع N مع العُقدة التافهة هو N: العُقدة التافهة هي إذن عنصر محايد بالنسبة للعملية، وتسمى عُقدة قابلة للفك إذا استطعنا كتابتها في شكل جمع عقدتين غير تافهتين.
العُقدة غير التافهة وغير القابلة للفك تسمى "لا تُفك" أو "أولية" ولاحظ تيه بالتجربة أن كل عقدة تفك بشكل وحيد كمجموع لعدد منتهى من العُقد الأولية، وهو ما لم يثبت إلا بعد وقت كبير على يد شوبرت 1949 Schubert.
لم يكن لدى تيه الطرائق التوبولوجية اللازمة لذلك الإثبات.
لقد نجح تيه مع شريكه كيركمان Kirkman في ترقيم العُقد الأولية التي لها 9 تقاطعات على الأكثر، ولقد ذكر العُقد غير الموجهة في جداوله تلك ولا يميز بين عُقدة وصورتها في المرآة.
لقد اتبع هذا المبدأ، التابعون لتيه الذين رقموا العُقد حتى 13 تقاطعا، ولا يوجد سوى عقدة وحيدة ذات ثلاثة تقاطعات هي الترفل.
وعقدة وحيدة ذات أربعة تقاطعات وهي 8 ويوجد 49 عقدة بتسعة تقاطعات لكل منها، حسب أعمال ثيستلثويت Thistelthwaite يوجد 9988 عقدة بـ 13 تقاطعا.
لقد كانت أعمال تيه وكيركمان تجريبية (مبنية على الملاحظة والاختبار) لم يرتبا بأي شكل لإثبات أن اثنين من العُقد مختلفتان، ولا العُقد غير تافهة إلا في بدايات القرن العشرين بفضل تقدم في التوبولوجي أصبحت هذه الإثباتات ممكنة.
ولقد اهتم تيه قبل كل شيء بالعُقد المتعاقبة بمعنى التي تُقبل بالرسم التخطيطي المتعاقد: ممر سفلي دائما ما يتعبه ممر علوي، ليس متعاقب بالإضافة إلى أن العُقد التي يمثلها ليست لها أي رسم تخطيطي متتالي، وإنه أحد الأمثلة الأكثر بساطة للعقدة غير المتعاقبة.
في الحقيقة إن كل العُقد أقل من 8 تقاطعات تكون متعاقبة، وكان لدى تيه عدة مبادئ لتصنيف العُقد المتتابعة. المقصود هنا الشروح التي كان متأكدا من صحتها دون أن يستطيع إثباتها، نسميها اليوم فرضيات تيه، ولقد فكر مثلا أن عدد التقاطعات جمعى أو بطريقة أخرى إذا كان N’; N عُقدتين.
فأن: C(N+N’)=C(N)+C(N’)
وهذا ما تم إثباته في عام 1987 على يد كوفمان Kauffman وميراسوجي Murasugi وثيستلثويت Thistlethwaite بالنسبة للعُقد المتعاقبة.
ولا زلنا لا نعرف إذا كانت هذه المعادلة صحيحة في حالة العُقد غير المتتابعة.
------ -- ------ -------- -------- -------- -------- --
المصادر:راجع حاشية هذا المقال.
ر
------ -- ------ -------- -------- -------- -------- --
المصادر:راجع حاشية هذا المقال.
ر



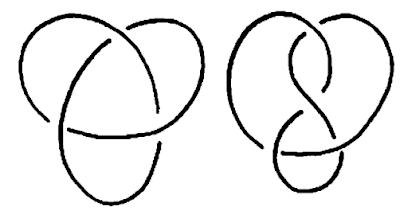










0 comments
إرسال تعليق